Видео: Ромбын диагональууд бие биенээ хуваадаг гэдгийг яаж батлах вэ?
2024 Зохиолч: Lynn Donovan | [email protected]. Хамгийн сүүлд өөрчлөгдсөн: 2023-12-15 23:50
Дотор ромб бүгд талууд тэнцүү, эсрэг талууд нь параллель байна. Цааш нь а ромб нь мөн параллелграмм тул a-ийн шинж чанарыг харуулдаг параллелограмм мөн тэр Параллелограммын диагональууд бие биенээ хоёр хуваасан.
Үүний дагуу ромбын диагональууд бие биенээ хуваадаг уу?
Аль ч тохиолдолд ромб , the диагональ (эсрэг булангуудыг холбосон шугамууд) бие биенээ хуваах зөв өнцгөөр (90 °). Тэр бол, диагональ бүр -ийг багасгадаг бусад хоёр тэнцүү хэсэгт хуваагдах ба тэдгээрийн огтлолцох өнцөг нь үргэлж 90 градус байна. Дээрх зураг дээрх хэлбэрийг өөрчлөхийн тулд дурын оройг чирнэ үү ромб мөн ийм байна гэж өөртөө итгүүл.
Хоёрдугаарт, ромб диагональууд перпендикуляр уу? А-ийн шинж чанарууд Ромб The диагональ байна перпендикуляр бие биендээ болон хуваах. Зэргэлдээх өнцгүүд нь нэмэлт (жишээлбэл, ∠A + ∠B = 180°). А ромб нь параллелограмм хэний диагональ байна перпендикуляр бие биедээ.
Үүнийг анхаарч үзвэл ромбын диагональууд перпендикуляр биссектриса гэдгийг хэрхэн батлах вэ?
Баталгаа тэр нь Ромбын диагональууд перпендикуляр байна Дээрх зүйлийн үргэлжлэл нотлох баримт : Тохирох гурвалжны харгалзах хэсгүүд нь тохирч байгаа тул бүх 4 өнцөг (дунд байгаа өнцөг) нь тэнцүү байна. Энэ нь тэдгээр нь бүгд 90 градустай тэнцүү байх явдалд хүргэдэг диагональ байна перпендикуляр бие биедээ.
Ромб параллелограмм мөн үү?
ТОДОРХОЙЛОЛТ: А ромб нь параллелограмм дөрвөн тохирох талтай. ТЕОРЕМ: Хэрэв a параллелограмм нь ромб , диагональ бүр нь эсрэг талын хос өнцгийг хуваана. ТЕОРЕМ Эсрэг: Хэрэв a параллелограмм эсрэг талын хос өнцгийг хуваах диагональуудтай, энэ нь a ромб.
Зөвлөмж болгож буй:
Ромбын диагональ гэж юу вэ?
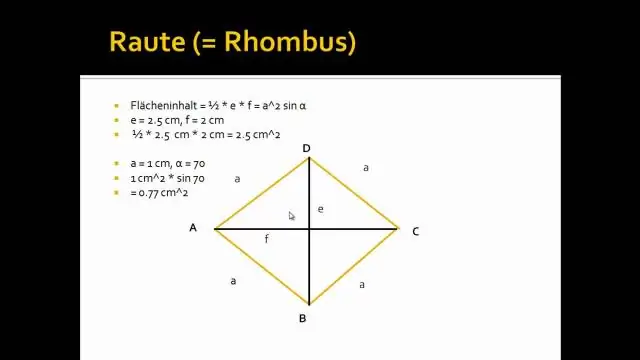
Ромбын диагональ Аливаа ромбуудад диагональууд (эсрэг булангуудыг холбосон шугамууд) зөв өнцгөөр (90°) хуваагддаг. Өөрөөр хэлбэл, диагональ бүр нөгөөг нь хоёр тэнцүү хэсэгт хуваадаг бөгөөд тэдгээрийн огтлолцох өнцөг нь үргэлж 90 градус байна
Таны загвар Overfitting гэдгийг яаж мэдэх вэ?
Загварын нарийвчлал нь загварыг сургахад ашигласан өгөгдлийн хувьд өндөр боловч шинэ өгөгдлөөр мэдэгдэхүйц буурч байгаа тохиолдолд хэт тохируулсан нь сэжигтэй байдаг. Загвар нь сургалтын өгөгдлийг сайн мэддэг боловч ерөнхийд нь нэгтгэдэггүй. Энэ нь загварыг урьдчилан таамаглах зэрэг зорилгод ашиггүй болгодог
Миний CPU бэлэн гэдгийг яаж мэдэх вэ?
Үүнийг нээхийн тулд Control Panel > System and Security > System руу очно уу. Та мөн энэ цонхыг шууд нээхийн тулд гар дээрх Windows+Pause товчлуурыг дарж болно. Таны компьютерийн CPU-ийн загвар болон хурдыг "Систем" гарчиг дор "Процессор"-ын баруун талд харуулна
Диагоналууд үргэлж параллелограмм дээр бие биенээ хуваадаг уу?
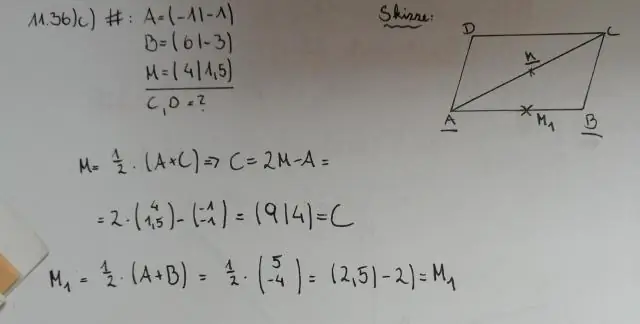
Аливаа параллелограммд диагональууд (эсрэг талын булангуудыг холбосон шугамууд) бие биенээ хуваадаг. Өөрөөр хэлбэл диагональ бүр нөгөөг нь хоёр тэнцүү хэсэгт хуваана. Дээрх зурагт параллелограммын хэлбэрийг өөрчлөхийн тулд дурын оройг чирж, энэ нь тийм гэдэгт өөрийгөө итгээрэй
Аль параллелограммууд бие биенээ хоёр хуваасан диагональтай вэ?
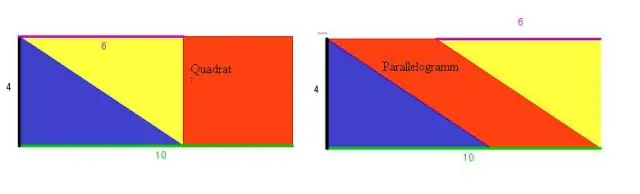
Хэрэв параллелограммын хоёр зэргэлдээ тал нь тэнцүү бол энэ нь ромб юм. Энэ туршилтыг ихэвчлэн ромбын тодорхойлолт болгон авдаг. Диагональууд нь зөв өнцгөөр хуваагдсан дөрвөн өнцөгтийг ромб гэнэ